
tictactoeia
Projet réalisé avec @guillaumeGRANDY dans le cadre du module d'Intelligence Artificielle/Apprentissage par renforcement en 4ème année à Polytech Lyon. Le but du projet était d'implémenter des algorithmes tels que min-max, alpha-beta et MCTS afin de jouer au morpion
Minimax VS Alpha-Beta
Les tests ci-dessous sont effectuées sur un plateau de 6x6 cases, soit 36 cases vides initialement. Chaque agent a une profondeur de 3. Pour les tests, nous avons d’abord fait une partie en faisant commencé minimax, puis on a ensuite interverti en faisant commencer alpha-beta. Cela nous a permis d’avoir le nombre d’états par tour pour les 2 joueurs.
En termes de nœuds crées
La courbe bleu et l’axe des ordonnées à droites et le nombre de cases vides par tour. C’est évidemment une fonction qui décroit car à chaque tour 2 pions sont ajoutés avec comme équation de droite y=- (numero_tour)+ nombre_de_cases_du_plateau
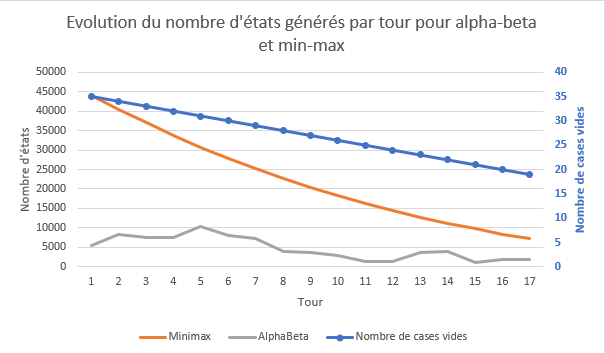
On voit que l’élagage de branches ajoutées dans Alpha Beta permet de limiter une exploration trop profonde et donc d’éviter la création de nouveaux états à explorer. Cela évite en plus de lancer une évaluation sur une branche qui ne nécessitait aucune évaluation.
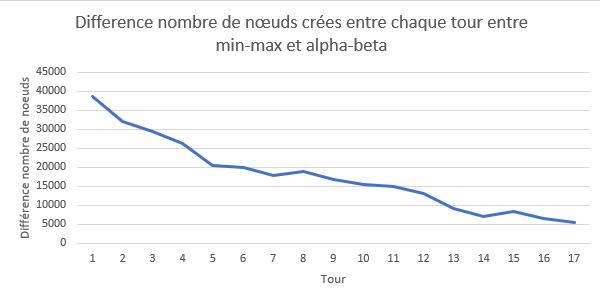
La différence de nombres d’états créés entre les 2 algos sur chaque tour est conséquente. Rien que sur le 1 er tour, on a entre 35 000 et 40 000 nœuds en moins qui ne sont pas créés pour l’algorithme alpha-beta.
En termes de temps d’exécution
Pour le temps d’exécution, on voit bien qu’Alpha-Beta est l’algorithme le plus rapide. En effet, beaucoup moins d’états sont explorés => le nombre d’appel de la fonction d’évaluations est donc forcément beaucoup moins important dans l’algorithme AlphaBeta. Etant donnée que l’on fait un parcours dans un tableau 2 dimensions, c’est la partie de l’algorithme qui peut faire perdre le plus de temps.
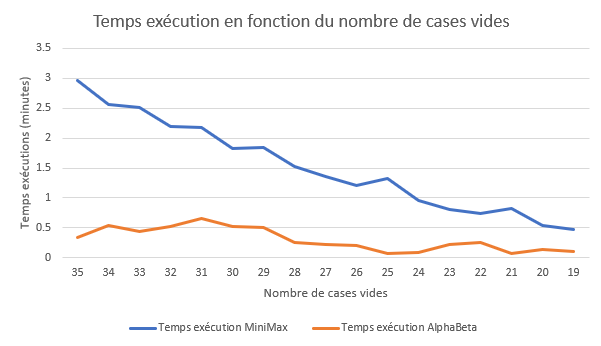
Performances agent contre agent
Alpha Beta / Min-Max
Afin de gagner du temps, nous avons estimer que les performances d’alpha-beta et min-max étaient similaires. En effet, le principe est le même pour les 2 algorithmes et ils donnent tout 2 le même résultat. Les seules différences sont que l’algorithme alpha-beta est plus optimisée et permet d’obtenir un résultat avec un temps d’exécution nettement inférieur à min-max (voir cette partie En termes de temps d’exécution) grâce au principe d’élagage de branches effectués par Alpha Beta.
Les fonctions d’évaluations mis en place
| Nom | Description |
|---|---|
| Eval2 | 10nombre_pions_alignées si on a un alignement de pions du même type qui peut être gagnant et -10nombre_pions_alignées pour les pions opposants |
| Eval3 | 10nombre_pions_alignées si on a un alignement de pions du même type qui peut être gagnant et -10nombre_pions_alignées pour les pions opposants 10taille_alignement_gagnant si on a un alignement de pions du même type qui est gagnant et -11taille_alignement_gagnant pour les pions opposants |
Sur la fonction d’évaluation 2, eval2, on s’est rendu compte que l’IA ne prenait pas en compte les récompenses immédiates. Voici un exemple ci-dessous pour illustrer notre propos.
🔴 Est le pion qu’on joue, et ✖️ est le pion adverse. Sur cette série de coup, 🔴 est le pion qui commence. Chaque grille est une étape de la partie jouée par les 2 joueurs avec 🔴 qui commence.
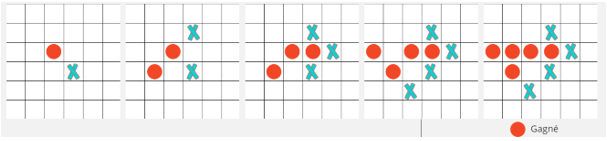
On voit à l’étape 4 que ✖️ préfère continuer sa diagonale commencée à l’étape 3 au lieu de bloquer 🔴 qui va gagner au prochain tour en alignant 4 pions 🔴
Cela nous a amené à mettre en place une nouvelle fonction d’évaluation 3, eval3. On a décidé de rajouter un score très élevé si on a la possibilité de gagner immédiatement et un malus > à ce score afin que l’IA évite au maximum de choisir des actions menant à une victoire immédiate de l’adversaire.
🔴 est le pion qu’on joue, et ✖️ est le pion adverse. Sur cette série de coup, 🔴 est le pion qui commence. Chaque grille est une étape de la partie jouée par les 2 joueurs avec 🔴 qui commence.
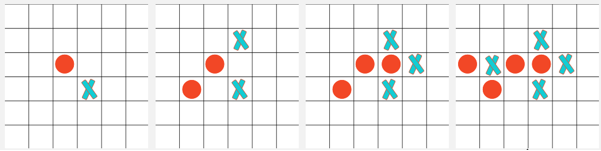
On voit qu’à l’étape 4, cette IA prend en compte le malus attribué à un état qui fait que l’adversaire peut gagner. Elle choisit donc de bloquer le prochain coup gagnant du joueur adverse.
Test IA contre adversaire multiple
Les essais ont été fait sur un tableau de taille 6x6 avec une taille de victoire de 4 pions alignés.
| Joueur 1 | Depth Joueur 1 | Type Joueur 2 | Depth Joueur 2 | Nombre partie | WinRate Joueur 1 | WinRate Joueur 2 | Egalité | Evaluation |
|---|---|---|---|---|---|---|---|---|
| Alpha Beta | 1 | Alpha Beta | 1 | 10 | 100% | 0% | 0% | eval3 |
| Alpha Beta | 1 | Alpha Beta | 2 | 10 | 0% | 100% | 0% | eval3 |
| Alpha Beta | 1 | Alpha Beta | 3 | 10 | 0% | 100% | 0% | eval3 |
| Alpha Beta | 2 | Alpha Beta | 1 | 10 | 100% | 0% | 0% | eval3 |
| Alpha Beta | 2 | Alpha Beta | 2 | 10 | 100% | 0% | 0% | eval3 |
| Alpha Beta | 2 | Alpha Beta | 3 | 10 | 0% | 0% | 100% | eval3 |
| Alpha Beta | 3 | Alpha Beta | 1 | 10 | 100% | 0% | 0% | eval3 |
| Alpha Beta | 3 | Alpha Beta | 2 | 10 | 100% | 0% | 0% | eval3 |
| Alpha Beta | 3 | Alpha Beta | 3 | 10 | 100% | 0% | 0% | eval3 |
| Alpha Beta | 1 | Coup aleatoire | Non applicable | 100 | 100% | 0% | 0% | eval3 |
| Alpha Beta | 2 | Coup aleatoire | Non applicable | 100 | 100% | 0% | 0% | eval3 |
| Alpha Beta | 3 | Coup aleatoire | Non applicable | 100 | 100% | 0% | 0% | eval3 |
| Joueur 1 | Depth Joueur 1 | Type Joueur 2 | Depth Joueur 2 | Nombre partie | WinRate Joueur 1 | WinRate Joueur 2 | Egalité | Evaluation |
|---|---|---|---|---|---|---|---|---|
| Alpha Beta | 1 | Alpha Beta | 1 | 10 | 100% | 0% | 0% | eval2 |
| Alpha Beta | 1 | Alpha Beta | 2 | 10 | 0% | 100% | 0% | eval2 |
| Alpha Beta | 1 | Alpha Beta | 3 | 10 | 0% | 100% | 0% | eval2 |
| Alpha Beta | 2 | Alpha Beta | 1 | 10 | 100% | 0% | 0% | eval2 |
| Alpha Beta | 2 | Alpha Beta | 2 | 10 | 100% | 0% | 0% | eval2 |
| Alpha Beta | 2 | Alpha Beta | 3 | 10 | 0% | 0% | 100% | eval2 |
| Alpha Beta | 3 | Alpha Beta | 1 | 10 | 100% | 0% | 0% | eval2 |
| Alpha Beta | 3 | Alpha Beta | 2 | 10 | 100% | 0% | 0% | eval2 |
| Alpha Beta | 3 | Alpha Beta | 3 | 10 | 100% | 0% | 0% | eval2 |
| Alpha Beta | 1 | Coup aleatoire | Non applicable | 100 | 100% | 0% | 0% | eval2 |
| Alpha Beta | 2 | Coup aleatoire | Non applicable | 100 | 100% | 0% | 0% | eval2 |
| Alpha Beta | 3 | Coup aleatoire | Non applicable | 100 | 100% | 0% | 0% | eval2 |
On remarque plusieurs choses :
Si la profondeur du joueur 1 et 2 sont identiques, le joueur 1 gagne car commencé en premier est un net avantage.
Si la profondeur du joueur 1 est inférieur à celle du joueur 2, le joueur 2 gagne ou les deux sont égalités