Projet_VRPTW

Le projet

Le problème de tournées de véhicules (appelé en anglais VRP Vehicle Routing Problem) est une classe de problème de recherche opérationnelle et d’optimisation combinatoire. Il s’agit de déterminer les tournées d’une flotte de véhicule afin de livrer une liste des clients. La variante que l’on a traité durant ce projet est la tournée de véhicule avec contraintes de capacité d’un véhicule (CVRP Capacited Vehicle Routing Problem). Chaque véhicule a une capacité maximum de colis qu’il peut livrer. Nous avions également une deuxième contrainte. Pour chaque client est imposé une fenêtre de temps dans laquelle la livraison doit être effectuée. Dans la suite de ce rapport, nous allons utiliser les termes suivants :

• Trajet : le trajet qu’effectue un camion pour livrer un certain nombre de clients, avec la contrainte que la somme des
• Tournée : ensemble des trajets effectués par les camions pour livrer l’ensemble des clients Pour traiter ce problème, nous avons suivi différentes phases :
• Import de la liste des clients à partir d’un fichier CSV
• Mise en place d’un algorithme naïf afin de générer une tournée
• Création des opérateurs de voisinage
• Développement d’une interface graphique afin de visualiser la localisation des clients et une tournée
• Mise en place de la méthode de descente afin de trouver un minimum local et tester nos opérateurs de voisinage
• Mise en place du Recuit simulé
• Mise en place de la méthode tabou

Conception

Nous avons décidé d’utiliser le patron de conception MVC (modèle vue contrôleur) afin de structurer notre projet. En ce qui concerne le code, nous avons décidé de tirer parti de la programmation objet afin de factoriser nos opérations usuelles : calcul de distance entre un client et un autre, entre un client et un dépôt, encapsulation de la capacité courante d’un camion dans une classe spécifique à un camion et utilisation d’opérations publiques afin de diminuer/augmenter cette dernière. Ces choix nous ont permis de limiter les effets de bords possibles, notamment lors de l’utilisation de ces classes dans les différents algorithmes que l’on utilise.

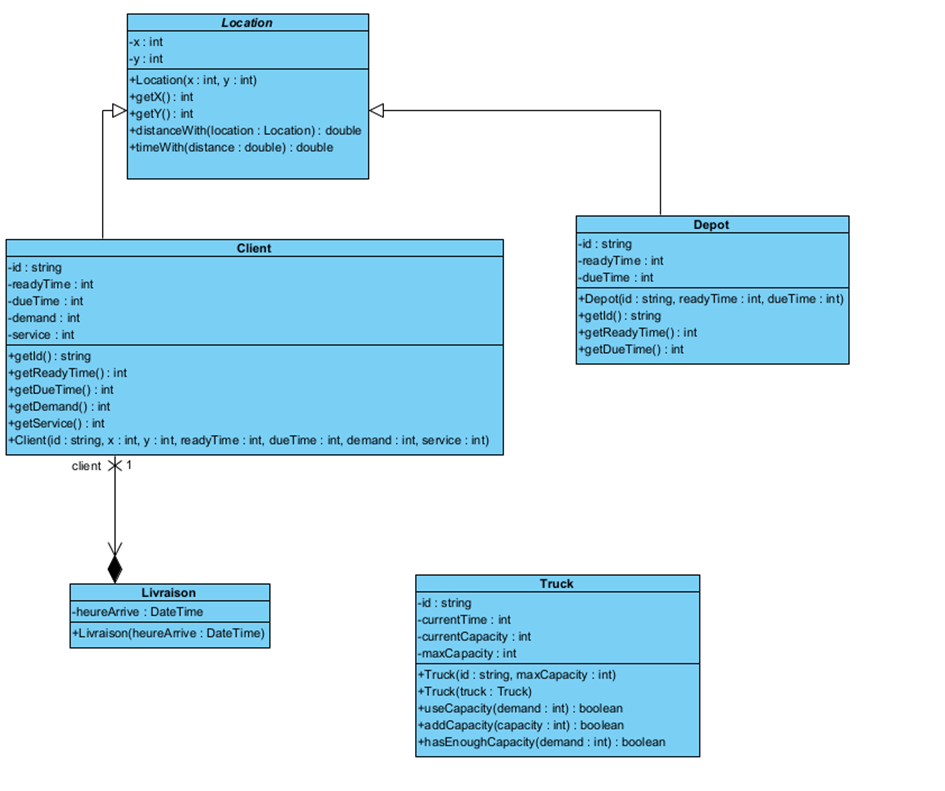
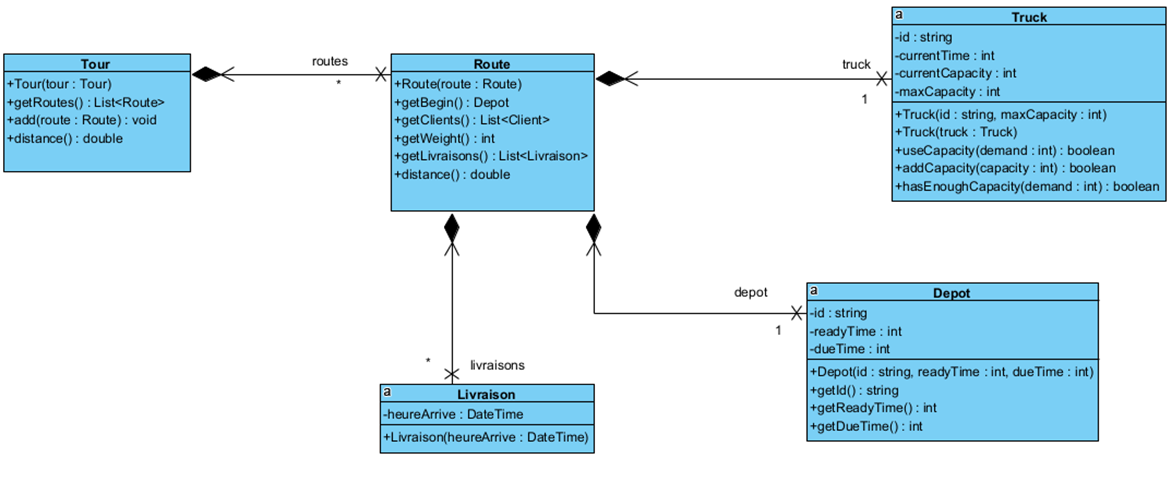
Nous avons décidé de modéliser l’ensemble des trajets effectués par les camions comme étant une tournée, un Tour. Un trajet effectué par un camion est une Route. Par cette modélisation, les opérateurs de voisinage sont encapsulés dans le Tour et la Route ce qui permet encore une fois de réduire les effets de bord possible par la manipulation de référence d’objet à travers plusieurs classes par exemple.

Enfin, en ce qui concerne les algorithmes de génération des tournées, nous avons décidé de modéliser de la façon suivante :

Pour les solutions initiales, tels que la génération aléatoire d’une tournée valide sur laquelle on peut appliquer des opérateurs de voisinage pour l’améliorer itérativement :

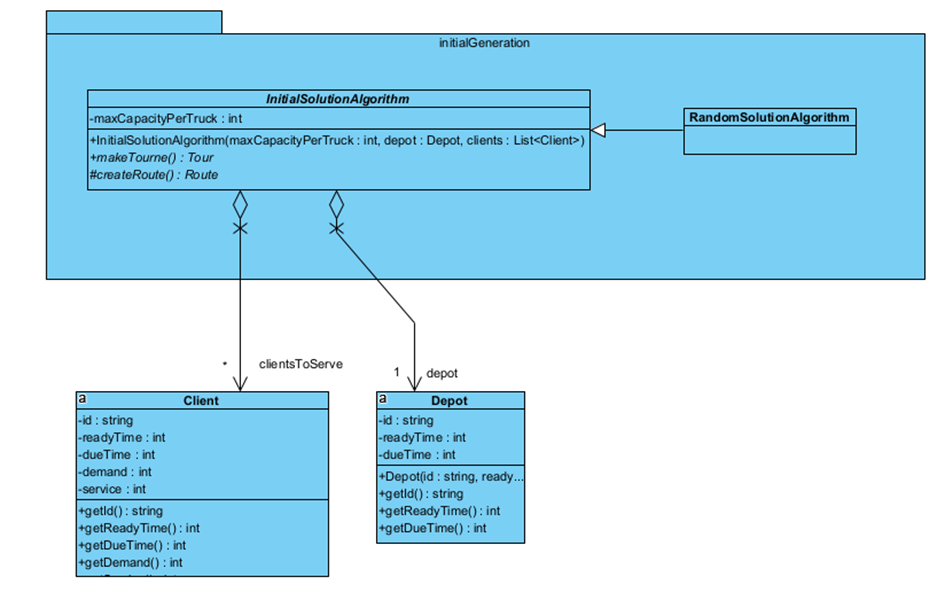
Nous avons une classe, RandomSolutionAlgorithm, qui permet de créer une Tournee avec la méthode makeTourne. Ensuite, nous avons commencé par faire de la recherche locale avec la méthode de descente

Nous avons créé une classe abstraite HillClimbing, en définissant la méthode localSearch qui itère récursivement sur le meilleur voisin d’une solution courant jusqu’à tomber dans un minimum local qui ne permet plus de trouver un meilleur voisin. Chaque classe fille de HillClimbing définisse la méthode exploreSiblings à partir d’une tournée courante passée en paramètre. Cette approche permet d’explorer tous les voisins pour trouver le meilleur parmi l’ensemble des voisins. Enfin, en ce qui concerne les métaheuristiques de recherche globale tel que le recuit simulé ou la méthode tabou, nous avons entrepris le choix de modéliser 2 classes spécifiques à ces 2 algorithmes. Elles sont localisées dans le package globalsearch.

Interface graphique

Pour simplifier la visualisation de la génération d’une tournée et de ses trajets, nous avons décidé de développer une interface graphique. Elle est développée en JavaFX, sans librairie annexe pour générer la carte des clients.

Vue générale de l’interface, avec la liste des clients à livrer sur la droite

Une fois qu’une tournée a été effectuée, on peut visualiser la liste des trajets de la tournée

En sélectionnant un trajet dans la liste, nous pouvons visualiser ce dernier graphiquement. Nous avons ajouté la même fonctionnalité pour les clients, nous pouvons visualiser où il se trouve graphiquement parmi la liste des clients à livrer.

Générateur des solutions aléatoires

Afin de générer la solution aléatoire, nous avons créé un algorithme qui trie aléatoirement la liste des clients à servir. Tant qu’il y a des clients à servir, nous prenons aléatoirement un client pour l’affecter au trajet courant s’il a encore de la place. S’il en a plus, nous créons un nouveau trajet. Enfin, quand il n’y a plus de clients à servir, nous retournons la tournée crée avec la liste des trajets à effectuer.

Opérateurs de voisinages

Lorsque nous avions créé une solution initiale générée aléatoirement, nous devions passer à son amélioration grâce aux méthodes à base de voisinage. Nous en avons donc créé un certain nombre sur la tournée qui sont des opérateurs axés sur des transformations entre trajet ainsi que sur les trajets qui sont des opérateurs axés sur des transformations internes à une tournée. Les principales difficultés rencontrées étaient sur les opérateurs de voisinage d’une tournée. En effet, lorsque l’on échange 2 clients qui sont situés sur 2 trajets différents, nous devons procéder à des vérifications sur la contrainte de poids et de fenêtre de temps des 2 trajets. Nous allons maintenant en revue tous les opérateurs que nous avons implémentés.

Métaheuristique

Recuit simulé

Sans fenêtre de temps

Les tests sont effectués sur les 30 premiers clients du fichier data101.vrp Afin de choisir les bons paramètres, nous avons commencé à faire des tests exhaustifs afin de choisir des paramètres donnant des tournées ayant les tournées les plus faibles.

On s’est vite rendu compte que c’était très complexe d’évaluer nos solutions. En effet, le recuit simulé fonctionne plus ou moins en fonction des paramètres choisie. Face à la complexité du choix des « bons paramètres », nous avons évalués de manière statistique l’évolution de la fitness en fonction de la variation de certains paramètres afin d’explorer les choix possibles pour ces derniers.

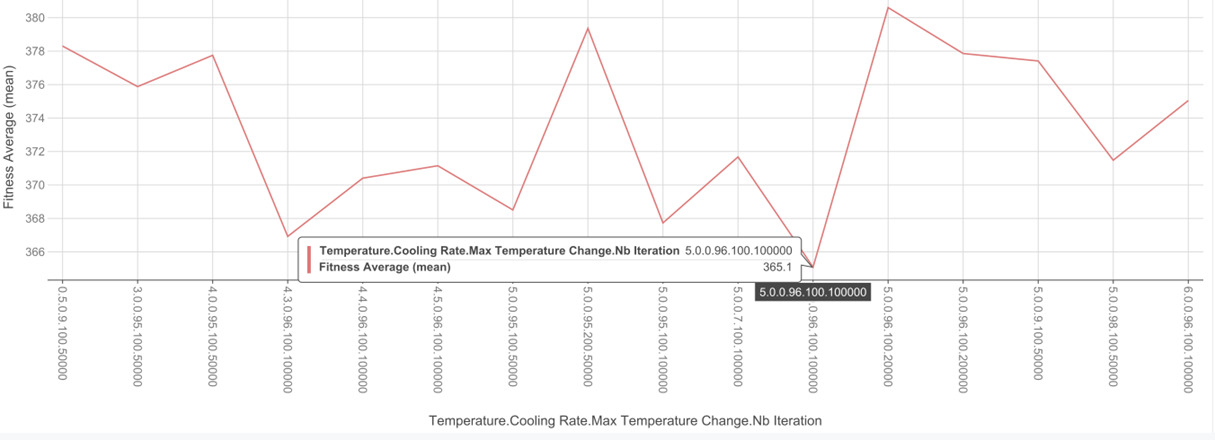
Sur le graphique ci-dessous, les valeurs en ordonnées sont la moyenne des fitness d’un échantillon de 5 solutions en partant d’une tournée initiale aléatoire. Nous avions choisi exhaustivement les paramètres de manière manuel.

Par la suite, on a décidé d’automatiser nos tests afin de lancer un grand nombre de fois le recuit simulé à partir de solutions initiales aléatoires en faisant varier certains paramètres dans des intervalles définies. Pour le graphique ci-dessous, nous avons fait varier les paramètres suivants :

• Le coefficient de décroissance : [0.1 ; 1] avec un pas de 0.05
• La température initiale : [0.5 ; 10] avec un pas de 0.5
• N1 le nombre de changement de températures : [10 ; 100] avec un pas de 5
• N2 fixé à 10 000

Pour tester s’il existe un échantillon de groupe de paramètres (mu, température initiale, N1) donnant en moyenne une fitness assez basse, nous devons donc générer toutes les permutations possibles de groupe de paramètre afin de trouver les groupes qui ont une influence sur la qualité d’une solution

Soit :

• $A$ : l'ensemble des valeurs choisies pour le coefficient de décroissance
• $B$ : l'ensemble des valeurs choisies pour la température initiale
• $C$ : l'ensemble des valeurs choisies pour le nombre de changement de température

Le nombre de permutations possibles est donc égal au produit cartésien des cardinaux des 3 ensembles :

$$\text{nombre de groupe de paramètres distincts possibles} = |A| \times |B| \times |C|$$

Pour notre ensemble de valeurs discrètes choisies précédemment, nous avons :

• $|A| = 20$
• $|B| = 19$
• $|C| = 19$

Soit : $\text{nombre de groupe de paramètres distincts possibles} = 20 \times 19 \times 19 = 7220$

Pour tester tous ces groupes de paramètres sur le recuit simulé, nous devons donc le lancer 7220 fois.

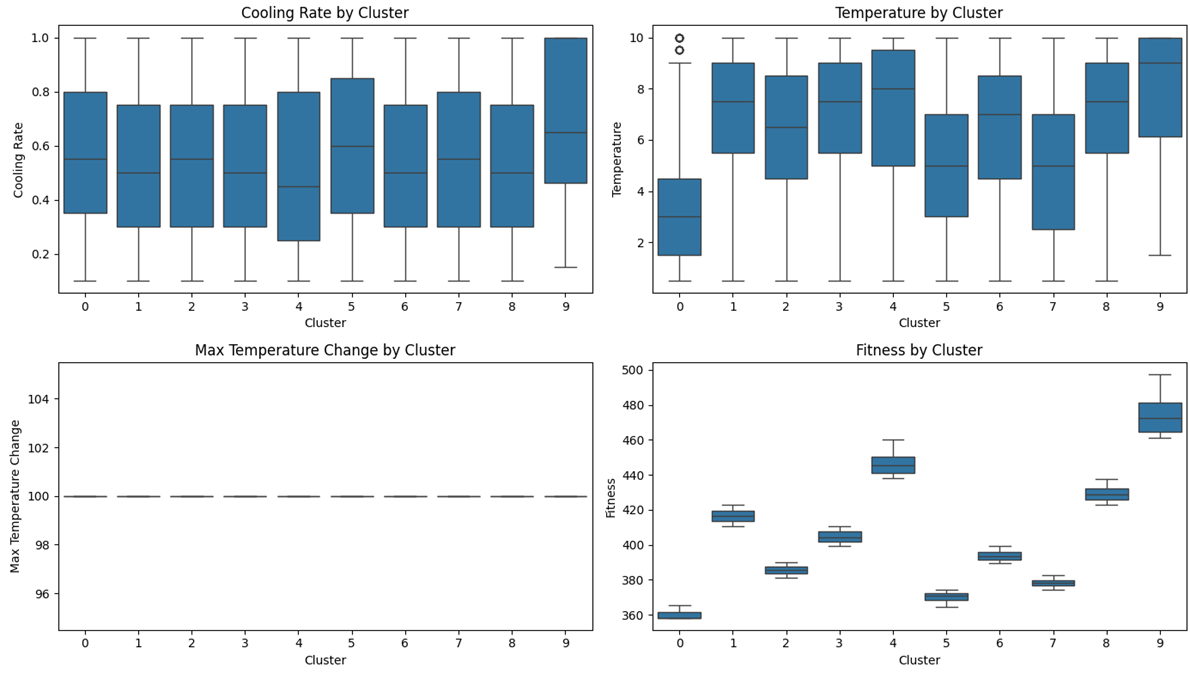
Sur le graphique ci-dessous, les points sont groupés par température. En abscisse, nous avons placé tous les paramètres du recuit simulé afin d'observer leur influence sur la fitness.

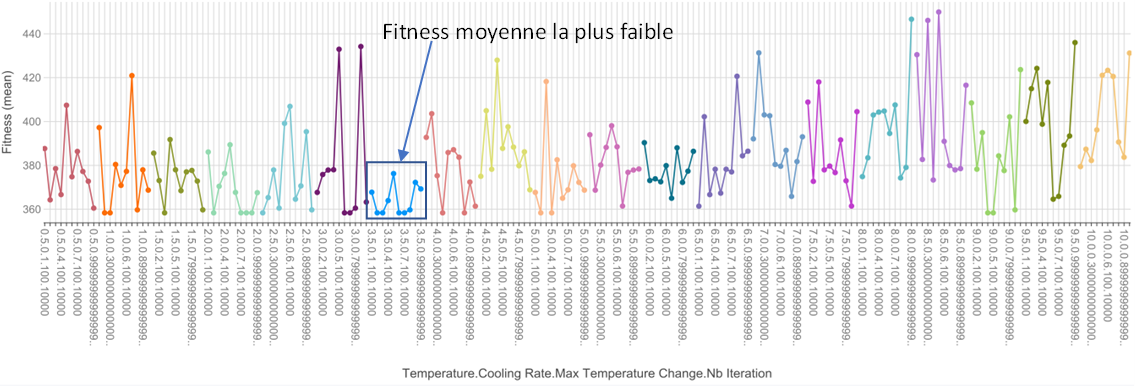
On voit que le groupe de paramètre en bleu ont une fitness moyenne très faible avec un écart type assez faible. On s’est rendu compte par la suite, que le problème avec le jeu de test précédent était que nous partons à chaque fois d’une même solution aléatoire. Les résultats pouvaient donc être biaisés. On a donc choisi de générer un nouvel échantillon de solutions en partant d’une nouvelle solution aléatoire à chaque utilisation du recuit simulé.

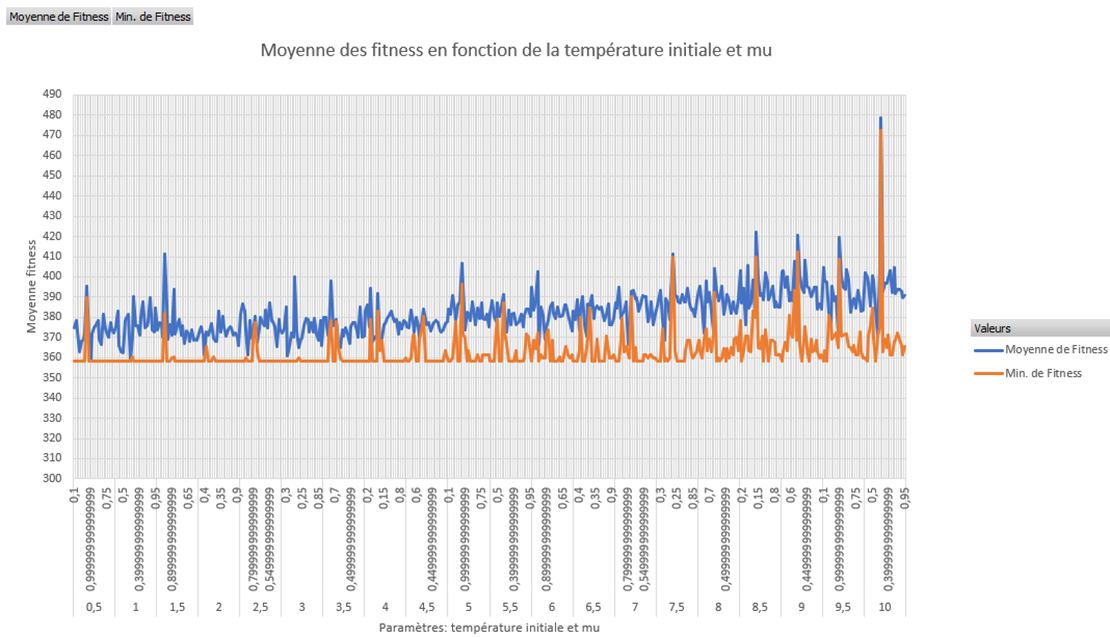
Par la suite, on a fait de la clusterisation avec l’algorithme des centres mobiles, afin de déterminer les groupes de paramètres permettant d’avoir le fitness la plus basse. On a remarqué la même chose que sur nos graphiques précédents. Plus la température est basse, plus la fitness est la plus basse.

Avec fenêtre de temps